تُعرف هذه المسألة بـ مشكلة جوزيفوس، وهي مشهورة جدًا.
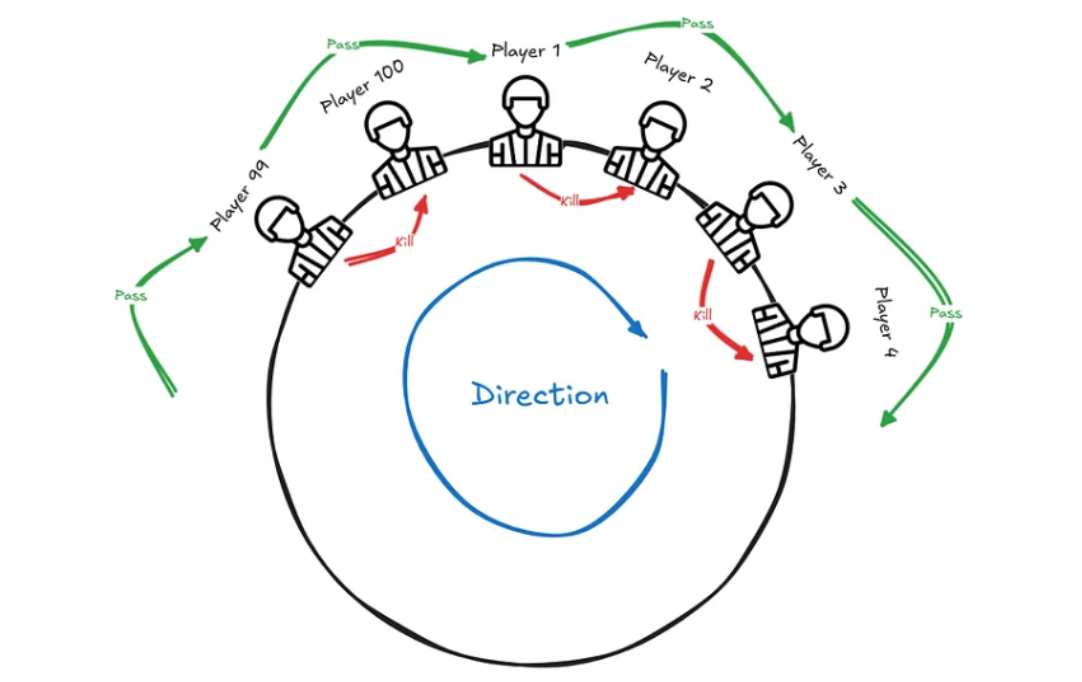
لنفرض انك استضفت 99 شخصا في بيتك، وكانت هنالك دجاجة واحدة أعطاها الملك لكم، ويجب أن يحصل عليها واحد فقط منكم بحسب ترتيب معين. فأي رقم ستختار من بين 1 إلى 100، لكي تبقى ويتم طرد الجميع؟
الفكرة هي العثور على طريقة تضمن بقاءك وحدك لتفوز بالدجاجة اللذيذة، وفقًا للقواعد التالية:
- تبدأ اللعبة بـ 100 لاعب. الرقم 1 يليه 2 وهكذا. والاتجاه ثابت طوال العملية.
- يحصل اللاعب رقم 1 على المقلاة، وبالتالي يخرج اللاعب المجاور له (اللاعب رقم 2).
- تنتقل المقلاة إلى اللاعب التالي (رقم 3)، ويخرج اللاعب الموالي له هو رقم 4، وتستمر الدورة بنفس الطريقة حتى يتبقى لاعب واحد فقط.
- يتم ترتيب اللاعبين في دائرة، ويبدأ الترتيب من الرقم 1 وحتى الرقم 100.
افتراض: يتم تخصيص الأرقام بناءً على أولوية الحضور، لنفرض أنك أول شخص يُطلب منه اختيار رقمه، مما يضمن عدم وجود تكرار للأرقام وأنك تحصل على الرقم الذي تختاره.
السؤال هو: أي رقم يجب أن تختار لتكون آخر لاعب يقف وتفوز بـ”عشاء الدجاج” اللذيذ؟
مساعدة:
تذكر انه توجد أرقام زوجية وأخرى فردية !
وأن هذا الوضع بترتيب.

💡 الحل
الطريقة الأولى
محاكاة العملية خطوة بخطوة:
- لنبدأ بمحاكاة العملية:
- الجولة الأولى: اللاعب رقم 1 يزيح اللاعب رقم 2، وتنتقل المقلاة إلى اللاعب رقم 3.
- تستمر العملية حتى يتبقى نصف اللاعبين.
- يتم تكرار العملية في الجولات التالية بنفس الطريقة، حتى يتبقى لاعب واحد فقط.
- الجولة الأولى: الصورة 02
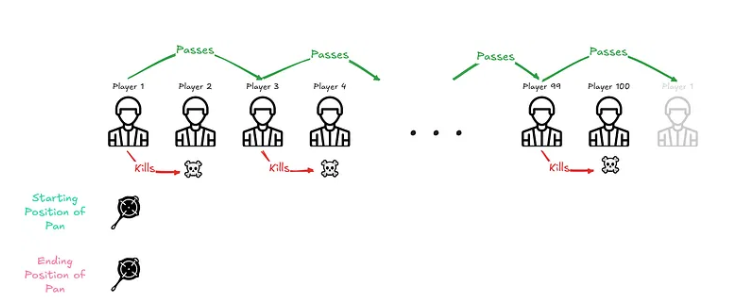
- اللاعبون المتبقين: 1, 3, 5, 7, … 99. (50 لاعبًا)
- المقلاة مع اللاعب 1.
- الجولة الثانية: الصورة 03
- اللاعبون المتبقون: 1, 5, 9, … 97. (25 لاعبًا)
- المقلاة مع اللاعب 1.
الجولة الثالثة الثالثة: الصورة 04
بعد الجولة الثالثة: الصورة 04
- اللاعبون المتبقون: 1، 9، 17، 25، 33، 41، 49، 57، 65، 73، 81، 89، 97.
- إجمالي اللاعبين المتبقين: 13 لاعبًا.
- المقلاة مع اللاعب: 97.
بعد الجولة الرابعة: الصورة 04
- اللاعبون المتبقون: 9، 25، 41، 57، 73، 89.
- إجمالي اللاعبين المتبقين: 6 لاعبين.
- المقلاة مع اللاعب: 9.
بعد الجولة الخامسة:
- اللاعبون المتبقون: 9، 41، 73.
- إجمالي اللاعبين المتبقين: 3 لاعبين.
- المقلاة مع اللاعب: 9.
بعد الجولة السادسة:
- اللاعبون المتبقون: 9، 73.
- إجمالي اللاعبين المتبقين: 2 لاعبين.
- المقلاة مع اللاعب: 73.
إذن، الرقم 73 هو الرقم الذي يجب اختياره لضمان البقاء اللاعب الأخير.
الطريقة الثانية
استخدام صيغة ثابتة:
بدلاً من محاكاة العملية التي تتطلب وقتًا كبيرًا نظرا لعدد اللاعبين الكبير، يمكن استخدام صيغة رياضية لحل المشكلة بشكل أسرع.
لكي يفوز اللاعب الذي يبدأ بالمقلاة، يجب أن يكون العدد الإجمالي للاعبين قوةً من 2 (مثل 2، 4، 8، 16…).
عندما يكون العدد الإجمالي غير قوة من 2، يمكننا تقريبه إلى أقرب قوة من 2 أصغر منه.
-
- المثال هنا:
- العدد الإجمالي 100.
- أقرب قوة من 2 هي 64.
- الفرق: 100 – 64 = 36.
- المثال هنا:
- إذن، اللاعب الذي يحمل المقلاة عند بداية الجولة التي تضم 64 لاعبًا هو اللاعب 73.
الصيغة العامة: