سؤال محير حول مقابلة الأرقام – ألغاز الأرقام مع الحل 1

سؤال مقابلة أرقام محير!
هل يمكنك حله في غضون 30 ثانية؟

الصورة (1)

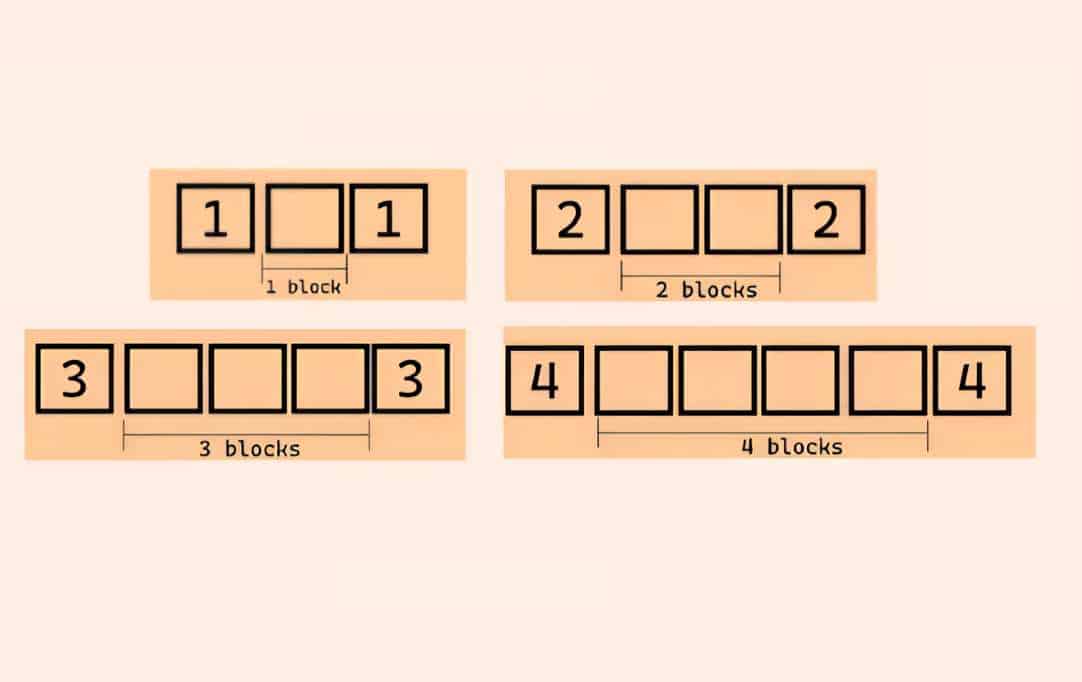
لديك ثمانية مكعبات مرقمة من 1 إلى 4، مع وجود مكعبين لكل رقم. قم بترتيب هذه المكعبات في ثمانية صناديق فارغة بحيث:

• المكعبان المرقمان بـ “1” يفصل بينهما مكعب واحد بالضبط.
• المكعبان المرقمان بـ “2” يفصل بينهما مكعبان بالضبط.
• المكعبان المرقمان بـ “3” يفصل بينهما ثلاثة مكعبات بالضبط.
• المكعبان المرقمان بـ “4” يفصل بينهما أربعة مكعبات بالضبط.

الصورة (4)

هذا سؤال شائع جدًا في مقابلات التوظيف في أمازون، وهو شائعًا للأدوار المتعلقة بهندسة البرمجيات حيث يُطلب منهم إنشاء ترتيب لانغفورد (Lanford Pairing) لعدد n من الأعداد الصحيحة، أو التحقق مما إذا كان ترتيب لانغفورد ممكنًا أم لا لعدد معين n من الأعداد.

من خلال فهم المبادئ الأساسية لهذه المشكلة، يصبح من الأسهل تصميم حل برمجي إذا كنت تطبق ذلك في مقابلة توظيف أو موقف مشابه.

كيف ستقوم بحل هذه المشكلة؟

الإجابة:

لا يمكن أن يكون هناك سوى إجابة واحدة!

لدينا ثماني صناديق فارغة يجب أن نملأها وفقًا لقواعد السؤال.
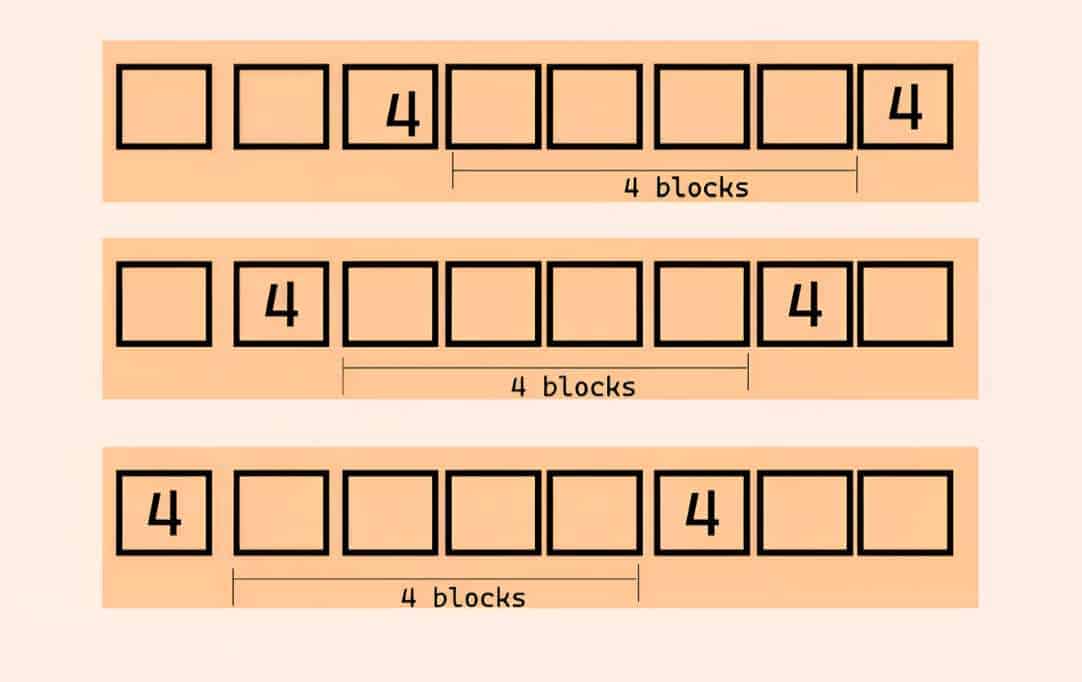
لنبدأ بالنظر في المواقع المحتملة لأكبر رقم، وهو الرقم 4.

تذكر أن كل رقم “4” يجب أن يكون مفصولًا عن الآخر بأربع مربعات.

الصورة (2)

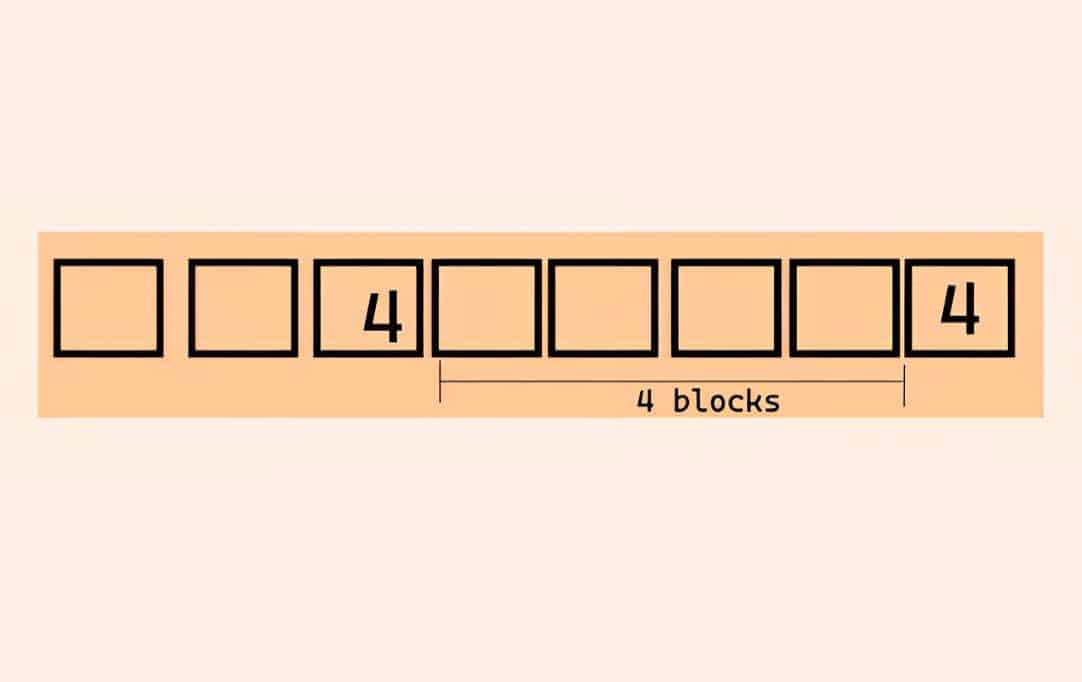
يمكننا تجربة أي من هذه الترتيبات الممكنة، ولكن في هذا الحل سنختار الترتيب الأول.

نظرًا لأنه الرقم الأول الذي نأخذه في الاعتبار، يُسمح لنا باختيار أي ترتيب ممكن، حيث نعتمد على عملية التجربة والخطأ.

الصورة (3)

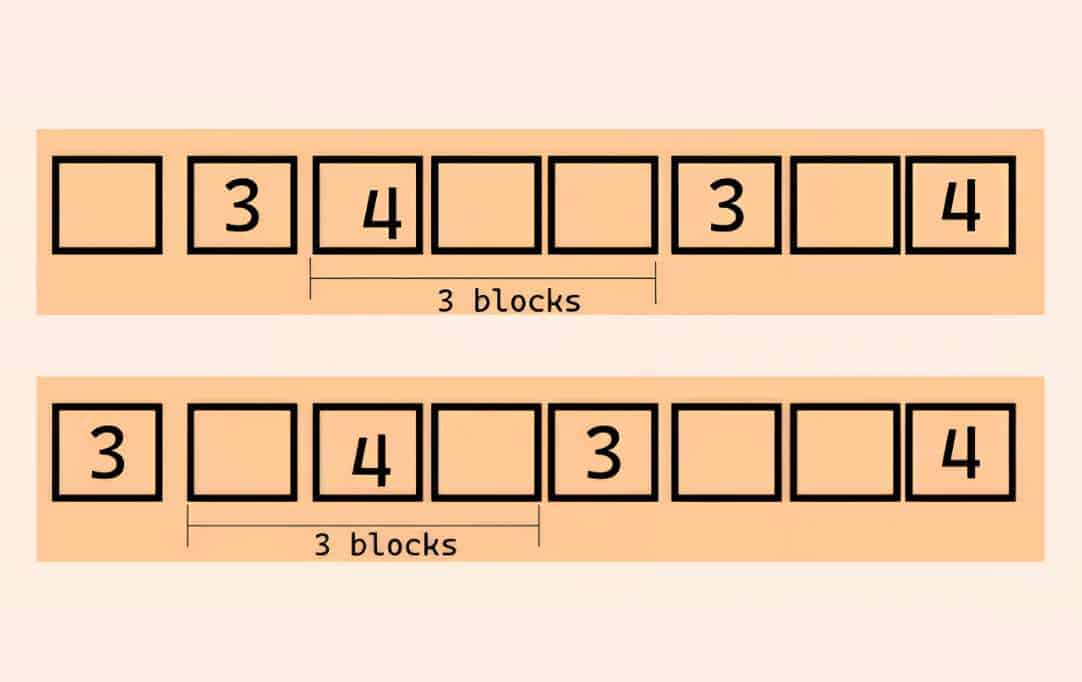
الآن بعد أن نظرنا في المواضع المحتملة للرقم 4، دعونا ننتقل إلى الرقم الجميل 3:

الصورة (5)

لدينا خياران ممكنان لوضع الرقم 3. لا يمكننا اختيار أي من هذه الخيارات عشوائيًا، بل يجب أن نأخذ في الاعتبار موضع الرقم 3 بحيث يتيح للرقم التالي، وهو 2، أن يتبع القاعدة المذكورة في السؤال.

بمجرد اختيارك للخيار المناسب تجد.

الصورة (6)