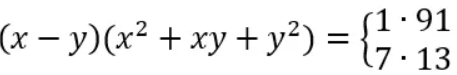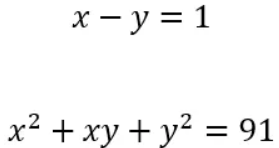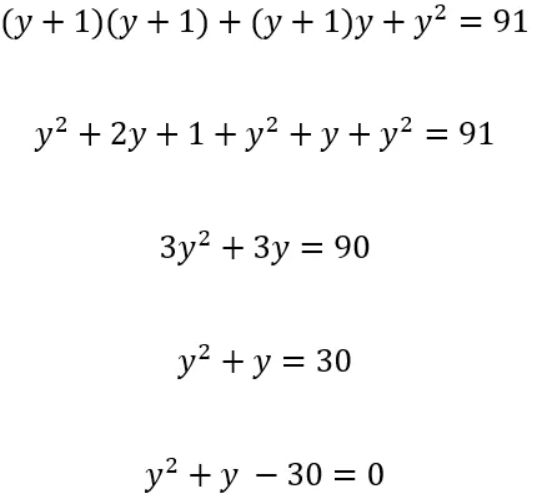هل يمكنك إيجاد قيم x و y في المعادلة التالية ؟
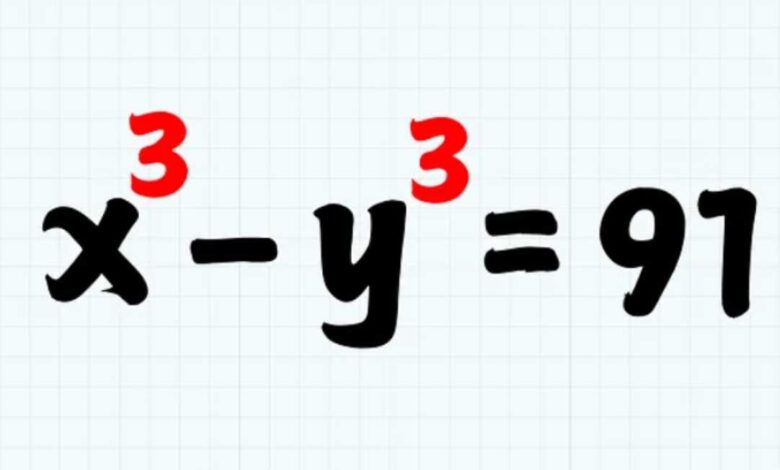
المطلوب هو إيجاد جميع القيم الممكنة لـ x و y بشرط أن تكون القيم عددين صحيحين موجبين؟
عند رؤية مسائل مثل هذه، أول ما أقوم به هو النظر إلى طرفي المعادلة ومحاولة التعبير عنهما كمنتجين لعوامل، ثم إجراء مقارنات.
هل لديك منهج مختلف؟
احضر قلمًا وورقة وحاول حلها بنفسك. دعنا نرى ما توصلت إليه في التعليقات!
حل المعادلة
المعادلة الأساسية هي:
الخطوة الأولى: تحليل الجانب الأيمن
الجانب الأيمن يمكن تفكيكه إلى 1 ضرب 91 أو 7 ضرب 13
الحالة الأولى
بالنظر إلى المعادلة فإن (x²+xy+y²) أكبر من (x-y).
وعلى الجانب الأيمن 91 أكبر من 1، سنجري مقارنة بين العوامل.
لنستبدل ذلك في المعادلة الثانية.
هذا يعطينا:
بإعادة الترتيب:
في هذه الحالة تكون قيمة y هي -6 أو 5 .
نظرًا لأن القيمة الموجبة هي فقط المقبولة، فإن y = 5.
تذكر أيضا أن x = 1 + y
هذا يعني أن x = 6 و y = 5.
للنظر الآن في الحالة الثانية:
بالنظر للمعادلة فإن الطرف x2+xy+y2 أكبر قطعا من x – y.
وفي الجانب الآخر 13 أكبر قطعا من 7
إذن يمكن ان نضع ما يلي
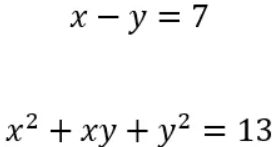
ستكون هنالك مشكلة إذا كان كل من x و y موجبين.
بما أن y ليست 0، إذن x يجب أن تكون أكبر من 7.
انظر إلى المعادلة الثانية بعناية. حتى لو x هو 7 ، فإن مربعها هو 49. حتى بدون التفكير في المصطلحات الأخرى ، فهي أكبر من 13 وهذا يجعل المعادلة غير صالحة.
لذلك ، سوف نتجاهل الحالة الثانية ، ونترك فقط (6 ، 5) كتركيبة صالحة ل x و y.
النتيجة النهائية
الحل الوحيد الممكن هو:
(x, y) = (6, 5)
رائع 👏